Question

A bag contains three dice, two of which are somewhat unusual: die A is a regular die whose faces show 1,2,3,4,5 and 6. Die B has a 4 on all 6 sides, and the faces of die C are2,2,4,4,6and 6. Suppose that a die is randomly selected, rolled, and comes up a 4. If the same die is rerolled, what is the probability that it is again a 4?

Answer 1

41/54

Explanation:

I will provide the approach and work it out. However, I am error prone, so check the arithmetic.

This is a Bayes Theorem problem.

Consider 3 "causes for a 4", Die A, B, or C, and an event, E.

The probability of each cause, given the event 4 is

`P(A|4)=(P(A)P(4|A))/(P(A)P(4|A)+P(B)P(4|B)+P(C)P(4|C))`

`P(B|4)=(P(B)P(4|B))/(P(A)P(4|A)+P(B)P(4|B)+P(C)P(4|C))`

`P(C|4)=(P(C)P(4|C))/(P(A)P(4|A)+P(B)P(4|B)+P(C)P(4|C))`

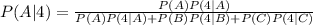
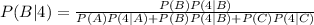
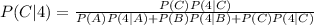
Since the rolled die is chosen at random,

P(A)=P(B)=P(C)=1/3

Also, from the numbers on the faces of each die,

P(4|A)=1/6

P(4|B)=1

P(4|C)=1/3

Making all the substitutions, we get

P(A|4)=1/9

P(B|4)=6/9

P(C|4)=2/9

That these sum to 1 is promising (maybe I didn't make a mistake).

Next we must roll the die again and the probability of a 4 could be because the die is A, B, or C. Thus, the desired probability is given by

P(A|4)P(4|A)+p(B|4)P(4|B)+P(C|4)P(4|C)

This evaluates to

(1/9)(1/6)+(6/9)(1)+(2/9)(1/3)=41/54

Answer 2

i dont know

Explanation: