Answer:
41/54
Explanation:
I will provide the approach and work it out. However, I am error prone, so check the arithmetic.
This is a Bayes Theorem problem.
Consider 3 "causes for a 4", Die A, B, or C, and an event, E.
The probability of each cause, given the event 4 is
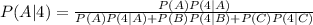
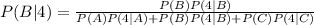
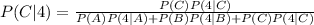
Since the rolled die is chosen at random,
P(A)=P(B)=P(C)=1/3
Also, from the numbers on the faces of each die,
P(4|A)=1/6
P(4|B)=1
P(4|C)=1/3
Making all the substitutions, we get
P(A|4)=1/9
P(B|4)=6/9
P(C|4)=2/9
That these sum to 1 is promising (maybe I didn't make a mistake).
Next we must roll the die again and the probability of a 4 could be because the die is A, B, or C. Thus, the desired probability is given by
P(A|4)P(4|A)+p(B|4)P(4|B)+P(C|4)P(4|C)
This evaluates to
(1/9)(1/6)+(6/9)(1)+(2/9)(1/3)=41/54