Answer:
see explanation
Explanation:
To show the points are collinear, that is lie on the same line.
Then the slope between A and B, B and C must be equal
Calculate slope m using the slope formula
m =
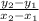
with (x₁, y₁ ) = A(- 3, - 1) and (x₂, y₂ ) = B(6, 5)
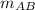 =
=
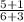 =
=
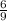 =
=

Repeat with (x₁, y₁ ) = B(6, 5) and (x₂, y₂ ) = C(3, 3)
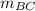 =
=
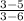 =
=
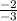 =
=

Since the slope between the 2 segments are equal and there is a common point B.
Then the points A, B and C are collinear