Question

A state Department of Transportation claims that the mean wait time for various services at its different location is more than 6 minutes. A random sample of 16 services at different locations has a mean wait time of 9.5 minutes and a standard deviation of 7.6 minutes. At α=0.05, what would be the outcome of a hypothesis test for this claim?

Answer 1

The hypothesis test reveals that at a 0.05 level of significance, there is sufficient evidence to support the claim that the mean wait time for services is more than 6 minutes, as the calculated t value exceeds the critical value.

Step-by-step explanation:

The student is asking about the outcome of a hypothesis test for the claim that the mean wait time for services is more than 6 minutes. Given the sample data, we will perform a one-sample t-test to determine if the mean wait time is significantly different from 6 minutes. The null hypothesis (H0) states that the mean wait time is 6 minutes or less, while the alternative hypothesis (Ha) claims that it is more than 6 minutes.

To conduct the test, we will use the following formula for the t statistic:

t = (sample mean - population mean) / (sample standard deviation / sqrt(sample size))

Substituting in the values:

t = (9.5 - 6) / (7.6 / sqrt(16))

t = 3.5 / (7.6 / 4) = 3.5 / 1.9 = 1.8421

The degrees of freedom for this test are 16 - 1 = 15. Looking up the critical t value for 15 degrees of freedom at the 0.05 level of significance, we find that the critical value for a one-tailed test is approximately 1.753. Since the calculated t value (1.8421) is greater than the critical value (1.753), we reject the null hypothesis.

Conclusion: At α = 0.05, there is sufficient evidence to support the claim that the mean wait time for services is more than 6 minutes.

Answer 2

At the 0.05 significance level, there is not enough evidence to conclude that the mean wait time for various services at different locations is more than 6 minutes.

To conduct a hypothesis test, we can use the following hypotheses:

Null Hypothesis (H0): The mean wait time is less than or equal to 6 minutes.

Alternative Hypothesis (Ha ): The mean wait time is more than 6 minutes.

Mathematically:

`H_a &: \mu > 6 \, \text{minutes} \end{split} \]`

Given data:

`s &= 7.6 \, \text{minutes} \, \text{(sample standard deviation)} \\n &= 16 \, \text{(sample size)} \\`

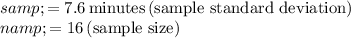
`\alpha &= 0.05 \, \text{(significance level)} \end{split} \]`

Now, we can calculate the test statistic and compare it to the critical value.

The test statistic
`(\(t\))` is given by:

`\[ t = \frac{(\bar{x} - \mu_0)}{(s/√(n))} \]`

where
`\(\mu_0\)` is the hypothesized population mean under the null hypothesis.

In this case,
`\(\mu_0 = 6\)` minutes.

`\[ t = ((9.5 - 6))/((7.6/√(16))) \]`

Now, we compare this \(t\)-value to the critical value from the t-distribution with
`\(df = n - 1 = 15\)` degrees of freedom at a significance level of 0.05.

If
`\(t > t_{\text{critical}}\)`, we reject the null hypothesis.

You can use a t-table or statistical software to find the critical value. Let's assume
`\(t_{\text{critical}} \approx 1.753\)` (this is just an example value, you should use the correct value based on the t-distribution table).

`\[ t \approx ((9.5 - 6))/((7.6/√(16))) \]`

`\[ t \approx (3.5)/((7.6/4)) \]`

`\[ t \approx (3.5)/(1.9) \approx 1.842 \]`

Since
`\(1.842 < 1.753\)`, we fail to reject the null hypothesis.

At the 0.05 significance level, there is not enough evidence to conclude that the mean wait time for various services at different locations is more than 6 minutes.