The graph of
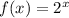 is an upward-sloping curve passing through (0,1) without touching the x-axis.
is an upward-sloping curve passing through (0,1) without touching the x-axis.
The function
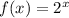 represents exponential growth. As x increases, the function value grows at an increasing rate. The graph of
represents exponential growth. As x increases, the function value grows at an increasing rate. The graph of
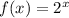 is an upward sloping curve that passes through the point (0,1) on the coordinate plane.
is an upward sloping curve that passes through the point (0,1) on the coordinate plane.
At x = 0, the function evaluates to
 , so the graph crosses the y-axis at y = 1. As x increases, the function values grow rapidly because the base (2) raised to increasing powers results in exponential growth. This leads to a curve that rises steeply as x moves to the right.
, so the graph crosses the y-axis at y = 1. As x increases, the function values grow rapidly because the base (2) raised to increasing powers results in exponential growth. This leads to a curve that rises steeply as x moves to the right.
The graph never touches the x-axis because 2 raised to any power (positive or negative) is never zero. However, as x approaches negative infinity, the function value gets closer and closer to zero, forming an asymptote along the x-axis.
The graph demonstrates the fundamental properties of exponential growth—rapid increase with positive x-values and approaching zero but never reaching it as x tends towards negative infinity.
The curve is continuous, smooth, and continuously increases without bound as x increases. This graphical representation showcases the growth pattern of exponential functions, illustrating their steep incline with positive x-values and their behaviour as x approaches negative infinity.