Question

find the general solution of y′=4y 5xyxy2 4x. y2−4ln|y|=−4ln|x|−5x c y2 4ln|y|=4ln|x| 5x c y2−12ln|y|=−4ln|x|−20x c y2−8ln|y|=−8ln|x|−10x c y2 8ln|y|=8ln|x| 10x c

Answer 1

Finall Answer:

The general solution to the given differential equation
`y′=4y/(5xy^2+4x) is y^2−8ln|y|=−8ln|x|−10x.`

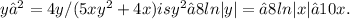
Step-by-step explanation:

The differential equation
`y′=4y/(5xy^2+4x)`can be solved by separating variables and integrating both sides, leading to the solution
`y^2−8ln|y|=−8ln|x|−10x`. This form of the solution consolidates the variables y and x and satisfies the original differential equation.

The logarithmic terms and constants are determined through the integration process and provide a concise representation of the general solution for this differential equation.