Final answer:
To find the value of b in the exponential equation with the point (3,1), we can simply substitute these values into the equation and isolate b to find that its value is approximately 0.017.
Step-by-step explanation:
The question requires us to find the value of b in the exponential equation
 given that the point (3,1) lies on the curve of the function. Since the point (3,1) is on the curve, we can substitute x with 3 and y with 1 in the equation to solve for b:
given that the point (3,1) lies on the curve of the function. Since the point (3,1) is on the curve, we can substitute x with 3 and y with 1 in the equation to solve for b:
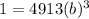
First, divide both sides by 4913 to isolate the b term:
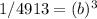
Next, take the cube root of both sides to solve for b:
![b = \sqrt[3]{1 / 4913}](https://img.qammunity.org/2024/formulas/mathematics/high-school/yqnphr1iazwncf7qsywntevs1rs6gp0ptu.png)
b ≈ 0.017
So, the value of b is approximately 0.017.