Question

An exponential function in the form y=4913(b)x contains the point (3,1). What is the value of b?

Answer 1

To find the value of b in the exponential equation with the point (3,1), we can simply substitute these values into the equation and isolate b to find that its value is approximately 0.017.

Step-by-step explanation:

The question requires us to find the value of b in the exponential equation
`y = 4913 (b)^x` given that the point (3,1) lies on the curve of the function. Since the point (3,1) is on the curve, we can substitute x with 3 and y with 1 in the equation to solve for b:

`1 = 4913 (b)^3`

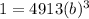
First, divide both sides by 4913 to isolate the b term:

`1 / 4913 = (b)^3`

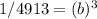
Next, take the cube root of both sides to solve for b:

`b = \sqrt[3]{1 / 4913}`

b ≈ 0.017

So, the value of b is approximately 0.017.