Final Answer:
The power rule states that the derivative of xⁿ with respect to x is
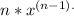
Step-by-step explanation:
The power rule is a fundamental rule in calculus used to find the derivative of a function that is a power of x. If we have a function f(x) = xⁿ, where n is a constant, the derivative f'(x) is calculated using the power rule.
Power Rule Formula:
According to the power rule, if f(x) = xⁿ, then f'(x) = n * x^(n-1).
Here, 'n' is the exponent of x, and the derivative is found by multiplying the exponent by the coefficient of x.
Example Calculation:
Let's consider the function f(x) = 3x². Applying the power rule, f'(x) = 2 * 3 * x^(2-1) = 6x.
In this example, the derivative of 3x² with respect to x is 6x.
Application:
The power rule is widely used to find derivatives of polynomial functions, making it a powerful tool in calculus.
It simplifies the process of finding derivatives, especially when dealing with functions involving powers of x.
Understanding and applying the power rule is essential for solving various calculus problems, especially when dealing with functions raised to different powers. It provides a systematic approach to finding derivatives and plays a crucial role in the study of calculus.