Final Answer:
The rate of change of the surface area of a sphere with respect to the radius is
 where
where
 is the radius.
is the radius.
Step-by-step explanation:
The surface area
 of a sphere is given by the formula
of a sphere is given by the formula
 where
where
 is the radius. To find the rate of change of \(A\) with respect to
is the radius. To find the rate of change of \(A\) with respect to
 we differentiate
we differentiate
 with respect to
with respect to
 :
:
![\[ (dA)/(dr) = (d)/(dr)(4πr^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/80ic6naz6p9l4kl2omtlpdojnlp856impc.png)
Using the power rule of differentiation, where
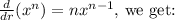
![\[ (dA)/(dr) = 8πr \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ei5j8m07ljrodf2xwrpgcgwwpchwu94fgt.png)
Therefore, the rate of change of the surface area of a sphere with respect to the radius is
 However, if you're looking for the instantaneous rate of change, you can substitute a specific radius value into the expression \(8πr\).
However, if you're looking for the instantaneous rate of change, you can substitute a specific radius value into the expression \(8πr\).
 to get the exact rate at that point.
to get the exact rate at that point.
In practical terms, this means that as the radius of a sphere increases, the surface area increases at a rate proportional to twice the radius. Understanding such rates of change is crucial in various applications, from physics to engineering, where the relationship between geometric properties of objects and their behavior is essential for analysis and design.