Question

This cone has a height of 27 centimeters and a diameter of 32 centimeters. What is the volume, in cubic centimeters, of the cone? Volume = cm3

can somebody help me with this.

Answer 1

The area of cone is 7240cm³.

Explanation:

Given that the diameter is 2 times greater than radius.

So the radius of this cone will be 16cm.

Next, we have to apply volume formula, V = (1/3)×(area of circle)×height.

Formula for area of circle is A = π×r² :

`V = (1)/(3) * \pi * {r}^(2) * h`

`V = (1)/(3) * \pi * {16}^(2) * 27`

`V = 7240 { \: cm}^(3) \: \: (3sf)`

Answer 2

The volume of cylinder is 7234.56 cm³.

Step-by-step explanation:

Given :

• 
  `\small\purple\bull` Height of cone = 27 cm.
• 
  `\small\purple\bull` Diameter of cone = 32 cm

To Find :

• 
  `\small\purple\bull` Radius of cone
• 
  `\small\purple\bull` Volume of cone

Using Formulas :

`\star{\small{\underline{\boxed{\sf{\pink{R = (D)/(2)}}}}}}`

• 
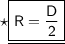
  `\blue\star` R = Radius
• 
  `\blue\star` D = Diameter

`\star{\small{\underline{\boxed{\sf{\pink{Volume_((Cone)) = (1)/(3)\pi{r}^(2)h}}}}}}`

• 
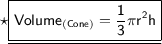
  `\blue\star` π = 3.14
• 
  `\blue\star` r = radius
• 
  `\blue\star` h = height

Solution :

Finding the radius of cone by substituting the values in the formula :

`\implies{\sf{Radius = (D)/(2)}}`

`\implies{\sf{Radius = (32)/(2)}}`

`\implies{\sf{Radius = \cancel{(32)/(2)}}}`

`\implies{\sf{\underline{\underline{\red{Radius = 16 \: cm}}}}}`

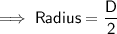
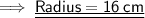
Hence, the radius of cone is 16 cm.

`\rule{200}2`

Now, finding the volume of cone by substituting the values in the formula :

`{\implies{\sf{Volume_((Cone)) = (1)/(3)\pi{r}^(2)h}}}`

`{\implies{\sf{Volume_((Cone)) = (1)/(3) * 3.14 * {(16)}^(2) * 27}}}`

`{\implies{\sf{Volume_((Cone)) = \frac{1}{\cancel{3}} * (314)/(100) * {(16 * 16)}* \cancel{27}}}}`

`{\implies{\sf{Volume_((Cone)) = (314)/(100) * 256 * 9}}}`

`{\implies{\sf{Volume_((Cone)) = (314)/(100) * 2304}}}`

`{\implies{\sf{Volume_((Cone)) = (314 * 2304)/(100)}}}`

`{\implies{\sf{Volume_((Cone)) = (723456)/(100)}}}`

`{\implies{\sf{\underline{\underline{\red{Volume_((Cone)) = 7234.56 \: {cm}^(3)}}}}}}`

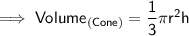
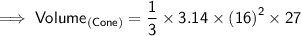
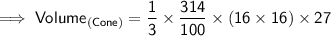
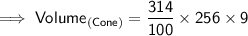
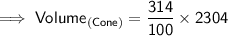
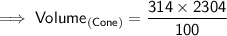
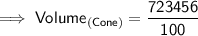
Hence, the volume of cone is 7234.56 cm³.

`\rule{300}{1.5}`