Question

Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the curves x = 4y², y ≥ 0, x = 4 about the axis y = 2?

Answer 1

The volume generated by rotating the region bounded by the curves x = 4y², y ≥ 0, x = 4 about the axis y = 2 is
`\( (32\pi)/(3) \).`

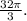
Step-by-step explanation:

To find the volume using the method of cylindrical shells, we integrate the circumference of the shell multiplied by its height. The integral bounds are determined by the intersection points of the curves
`\(x = 4y^2\) and \(x = 4\) which occur at \(y = 0\) and \(y = 1\).`

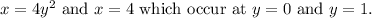
The radius of the cylindrical shell is given by
`\(r = x - 4\)`. The height of the shell is
`\(h = 2 - y\)`. The circumference of the shell is
`\(2\pi r\),` so the volume element is
`\(2\pi r h\).`

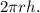
The integral setup is:

`\[V = \int_(0)^(1) 2\pi (4y^2 - 4)(2 - y) \,dy\]`

Simplifying the expression, we get:

`\[V = \int_(0)^(1) 2\pi (8y^3 - 4y^2 - 8y + 4) \,dy\]`

Integrating with respect to
`\(y\),` we find:

`\[V = (32\pi)/(3)\]`

The final answer,
`\( (32\pi)/(3) \)`, represents the volume of the solid obtained by rotating the region about the given axis.