Question

Write the system of linear equations in the form ax = b and solve this matrix equation for x.

Answer 1

To solve the given system of linear equations using a matrix equation, we first write the equations in matrix form as A*X = B. Then, we find the inverse of matrix A and multiply it by matrix B to solve for the vector X, which contains the values of the variables x₁ and x₂.

Step-by-step explanation:

To write the system of linear equations in the form ax = b and solve this matrix equation for x, we start by setting up the equations given:

Equation 1: -2x₁ - 3x₂ = -26

Equation 2: 6x₁ + x₂ = -42

The corresponding matrix form ax = b can be represented as:

`A =| -2 -3 || 6 1 |\\,X =| x₁ || x₂ |,\\B =|-26||-42|`

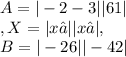
The matrix equation is then A * X = B.

To solve for X, we can use matrix algebra, particularly the inverse of matrix A, if it exists. We calculate the inverse of A, and then multiply it by B to get X.

Solution Steps:

1. Find the inverse of matrix A (A^{-1} if it exists).
2. Multiply the inverse of A by matrix B (X = A^{-1}B).
3. Solve for the values of x₁ and x₂.

Upon solving, we would get specific values for x₁ and x₂ that satisfy both equations.

Complete question is as follows :

Write the system of linear equations in the form ax = b and solve this matrix equation for x.

-2x₁-3x₂=-2

6x₁+x₂=-42