Final answer:
To solve the given system of linear equations using a matrix equation, we first write the equations in matrix form as A*X = B. Then, we find the inverse of matrix A and multiply it by matrix B to solve for the vector X, which contains the values of the variables x₁ and x₂.
Step-by-step explanation:
To write the system of linear equations in the form ax = b and solve this matrix equation for x, we start by setting up the equations given:
Equation 1: -2x₁ - 3x₂ = -26
Equation 2: 6x₁ + x₂ = -42
The corresponding matrix form ax = b can be represented as:
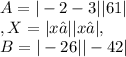
The matrix equation is then A * X = B.
To solve for X, we can use matrix algebra, particularly the inverse of matrix A, if it exists. We calculate the inverse of A, and then multiply it by B to get X.
Solution Steps:
- Find the inverse of matrix A (A^{-1} if it exists).
- Multiply the inverse of A by matrix B (X = A^{-1}B).
- Solve for the values of x₁ and x₂.
Upon solving, we would get specific values for x₁ and x₂ that satisfy both equations.
Complete question is as follows :
Write the system of linear equations in the form ax = b and solve this matrix equation for x.
-2x₁-3x₂=-2
6x₁+x₂=-42