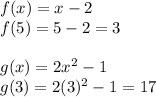Answer:
(a.): There is no inverse of g(x). 2x^(2)-1 is not a one-to-one function, meaning there is not one x for every y (on a graph, you can apply the horizontal line test and see that the graph crosses the same x-coordinate for many y-coordinates twice). Thus, it does not have an inverse
(b.): f(h(-2)) = -14
(c.): g(f(5)) = 17
Explanation:
(a.): g(x) = 2x^(2) - 1 is not a one-to-one function, meaning there is not one x for every y (on a graph, you can apply the horizontal line test and see that the graph crosses the same x-coordinate for many y-coordinates twice). Thus, it does not have an inverse.
(b.) To find f(h(-2)), we first plug in -2 as the input for h(x). Then, this output becomes the input for f(x):
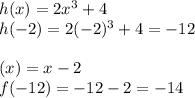
(c.) To find g(f(5)) we first plug in 5 as the input for f(x). Then, this output becomes the input for g(x):