Final answer:
The top speed at which the five clowns can successfully drive around the curve is approximately 15.21 m/s.
Step-by-step explanation:
To calculate the top speed at which the five clowns can successfully drive around the curve, we need to use the formula for centripetal force:
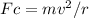
Where Fc is the centripetal force, m is the mass, v is the speed, and r is the radius of the curve.
We know the radius is 27.5 m, and the coefficient of friction is 0.8. The maximum frictional force can be calculated using the formula:
fmax = µN
Where fmax is the maximum frictional force, µ is the coefficient of friction, and N is the normal force. The normal force can be calculated using the equation:
N = mg
Where m is the mass of the car and g is the acceleration due to gravity.
By equating the centripetal force and maximum frictional force, we can solve for the maximum speed:
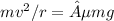
Simplifying the equation gives:
v = sqrt(µgr)
Plugging in the values, we get:
v = sqrt(0.8 * 9.8 * 27.5)
v ≈ 15.21 m/s