Question

Trapezoid ABCD has vertices A(-5,9) B(-2,9) C(-8,0) D(1,0) after a translation of 2 units right and 3 units down followed by a dilation with a scale factor of 2/3. What are the vertices of trapezoid RSTU

Answer 1

(-2,4), (0,4), (-4,-2) and (2,-2)

Explanation:

Given

`A = (-5,9)`

`B = (-2,9)`

`C = (-8,0)`

`D = (1,0)`

`Translation: 2\ units\ right\ \& \ 3\ units\ down`

`Dilation: (2)/(3)`

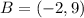
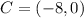
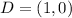
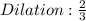
Required

Determine the vertices of the image RSTU

When a coordinate (x,y) is translates b units right, the new coordinate is: (x + b, y)

So, translation 2 units right gives:

`A = (-5,9)` --->
`A' = (-5 + 2,9) = (-3,9)`

`B = (-2,9)` --->
`B' = (-2 + 2,9) = (0,9)`

`C = (-8,0)` --->
`C' = (-8 + 2,0) = (-6,0)`

`D = (1,0)` --- >
`D' = (1 + 2,0) = (3,0)`

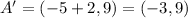
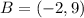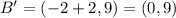
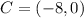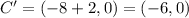
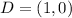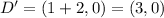
When a coordinate (x,y) is translates b units down, the new coordinate is: (x, y-b)

So, translation 3 units down gives:

`A' = (-3,9)` --->
`A`

`B' = (0,9)` -->
`B`

`C' = (-6,0)` -->
`C`

`D' = (3,0)`-->
`D`

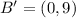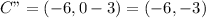
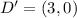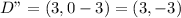
Lastly, dilation of 2/3 gives:

`New = Old * (2)/(3)`

`R = (-3,6) * (2)/(3) = (-2,4)`

`S = (0,6) * (2)/(3) = (0,4)`

`T = (-6,-3) * (2)/(3) = (-4,-2)`

`U = (3,-3) * (2)/(3) = (2,-2)`

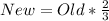
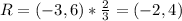
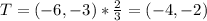
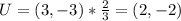
Hence, the coordinates of RSTU are: (-2,4), (0,4), (-4,-2) and (2,-2)