Final answer:
a)
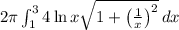
b)
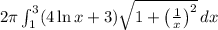
c)
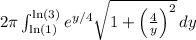
Step-by-step explanation:
a) About the x-axis:
The formula to find the surface area generated by rotating the curve
 from
from
 about the x-axis is given by the surface area integral:
about the x-axis is given by the surface area integral:
![\[ A = 2\pi \int_(a)^(b) f(x) √(1 + [f'(x)]^2) \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9h8kuqfajaw6wwzleofrnm2di6ynubnv22.png)
Here,
 .
.
![\[ A_x = 2\pi \int_(1)^(3) 4 \ln x \sqrt{1 + \left((1)/(x)\right)^2} \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1o2c50anmd3dtu6y8df04tjyxbf3s1k547.png)
b) About the line y = −3:
The formula for the surface area when rotating the curve about the line
 is:
is:
![\[ A = 2\pi \int_(a)^(b) [f(x) - (-3)] √(1 + [f'(x)]^2) \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zqx1mg1m1j39zsmwn9e4y6r0o3kyqfagmd.png)
![\[ A_y = 2\pi \int_(1)^(3) (4 \ln x + 3) \sqrt{1 + \left((1)/(x)\right)^2} \, dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yfqtucg3qymaxmms1hvui3clkae6g5f5qq.png)
c) About the line x = −3:
When rotating about the line
 , the formula is:
, the formula is:
![\[ A = 2\pi \int_(a)^(b) f(y) √(1 + [f'(y)]^2) \, dy \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lc05fbht5dhctxxiuwztzgxn6dw1umjeji.png)
Here,
 is the inverse function of
is the inverse function of
 , which is
, which is
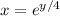 . The derivative
. The derivative
 is found accordingly.
is found accordingly.
![\[ A_(x=-3) = 2\pi \int_(\ln(1))^(\ln(3)) e^(y/4) \sqrt{1 + \left((4)/(y)\right)^2} \, dy \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/491r6rtmmme99gvokvf81bo7y369sim6zk.png)
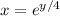
These integrals represent the surface area for rotation about the x-axis, y-axis, and a vertical line x = -3, respectively. Please note that the integrals themselves would need to be solved to find the numerical values.