Question

A tree 16 feet tall casts a shadow which forms an angle of 40° with the ground. How long is the shadow to the nearest hundredth of a foot?

Answer 1

x = 19.06 feet

Explanation:

Given that,

The length of a tree, h = 16 feet

It casts a shadow which forms an angle of 40° with the ground.

We need to find the length of the shadow. We can find it using trigonometry such that x be the length of the shadow. So,

`\tan\theta=(h)/(x)\\\\x=(h)/(\tan\theta)\\\\x=(16)/(\tan(40))\\\\x=19.06\ \text{feet}`

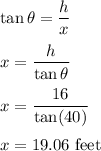
So, the length of the shadow is 19.06 feet.