The claim is rejected.
How to test the validity of a claim using one tailed test.
Given that the
population size, n = 196
success = 90
Alpha level = 0.01
The null hypothesis (H0) is that the population proportion (p) is greater than or equal to 0.05, and the alternative hypothesis (H1) is that the population proportion is less than 0.05.
The proportion, p = success/population size
p = 90/196 = 0.46
Null hypothesis (H0): P >= 0
Alternative hypothesis (H1) : p < 0
Let's calculated z-statistic
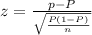
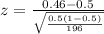
z = -0.04/0.04 = -0.01
p- value = p(Z<z-statistic )
= p(z-1)
From table
p- value = 0.159
If the z-statistic is less than the critical value, we would reject the null hypothesis in favor of the alternative.
The p - value is 0.159 which is greater than critical p-value.
Therefore, the claim is rejected.
Complete question
Test whether the population proportion is less than 0.5. A random sample of size 196 yields 90 successes. Let a=0.01