Question

Example 2 - A ball is thrown straight up from the top of a 288 foot tall building with an

initial speed of 48 feet per second. The height of the ball as a function of time can be
modeled by the function h(t) = -16t? +48t + 288. When will the ball reach a height of 320
feet?

Answer 1

step 1. h(t) = -16t^2 + 48t + 288. Set this equal to 320.

step 2. -16t^2 +48t + 288 = 320

step 3. -16t^2 + 48t - 32 = 0

step 4. -16(t^2 - 3t + 2)

step 5. -16(t - 2)(t - 1)

step 6. The ball reaches 320 feet "both!!!" at t = 1, 2 seconds once going up and once coming down.

Answer 2

The ball will reach a height of 320 feet at t = 1 second and t = 2 seconds.

To find when the ball reaches a height of 320 feet, we need to set the function

h(t) equal to 320 and solve for t.

The given function is

h(t)=−16
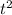`t^(2)`+48t+288, so we set it equal to 320:

−16
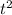`t^(2)`+48t+288=320

Now, we can rearrange the equation to form a quadratic equation in standard form:

−16
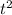`t^(2)`+48t−32 = 0

To solve this quadratic equation, you can use the quadratic formula:

t= −b±
`\sqrt{ b^(2) - 4ac}` / 2a

​For our equation, a=−16, b=48, and c=−32. Substituting these values into the formula:

t= −48±
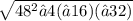`\sqrt{48^(2) −4(−16)(−32) }`/ 2(−16)

​Simplify further:

t = −48±
`√(2304 - 2048)` / -32

t= −48±
`√(256)` /−32

t = −48±16 / -32

​Now, we have two possible solutions for

t1 = -48+16 / -32

t2 = -48-16/-32

Calculate each value to find the corresponding time when the ball reaches a height of 320 feet. Keep in mind that negative time values may not be physically meaningful in this context, so consider only the positive solutions.

t1 = -32/-32 = 1

t2 = -64/-32 = 2

So, the ball will reach a height of 320 feet at

t=1 second and

t=2 seconds.