The polynomial shown in the graph is the first option:
g(x) = (x - 1)²*(x +2)
Which function is shown in the graph?
Ok, for a polynomial, if the graph just passes through the x-axes like in the left intercept, then the multiplicity of that zero is odd.
If it passes through the x-axis like in the right intercept (so we have like the vertex of a parabola) then we have an even multiplicity.
Remember that if a polynomial has zeros x = h, and x = k, then the equation:
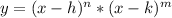
Means that the multiplicity of h is n, and the multiplicity of k is m.
From this, we can see that:
- The zero at x = -2, must have odd multiplicity.
- The zero at x = 1, must have even multiplicity.
Then the correct option is:
g(x) = (x - 1)²*(x +2)