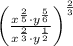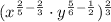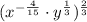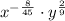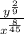The simplified form of algebraic expressions are now shown:
Case 1:
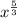
Case 2:
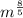
Case 3:
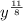
Case 4:
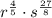
Case 5:
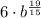
Case 6:
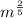
Case 7:
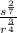
Case 8:
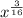
Case 9:
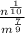
Case 10:
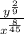
How to simplify algebraic expressions by power properties
In this problem we need to simplify algebraic expressions by power properties, which are introduced below:
Product of two powers:
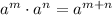
Division of two powers:
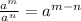
Power of a power:
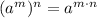
Further power properties:
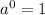
Now we proceed to simplify each expression by means of power properties:
Case 1:
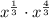
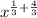
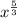
Case 2:
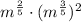
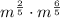
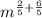
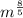
Case 3:
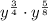
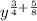
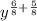
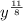
Case 4:
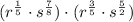
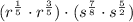
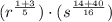
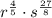
Case 5:
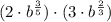
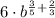
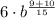
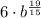
Case 6:
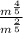
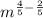
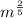
Case 7:
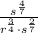
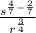
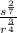
Case 8:
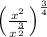
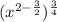
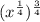
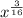
Case 9:
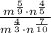
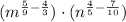
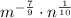
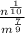
Case 10: