Question

A 15 g arrow is accelerated by a bow over a distance of 46.7 cm to a speed of 73.7 m/s.

Use the work-energy theorem to find the average force exerted on the arrow while it is being accelerated.

Answer 1

Approximately
`87.2\; {\rm N}`.

Step-by-step explanation:

By the Work-Energy Theorem, the change in the kinetic energy of this arrow should be equal to the work that the resultant force did on the arrow. If the force from the bow is the only force on this arrow, the change in the kinetic energy of the arrow would be equal to the force that the bow exerted.

The average force exerted on the arrow can be found in the following steps:

• Find the change in the kinetic energy of the arrow, which would be equal to the amount of work that the bow did on the arrow.
• To find the average force the bow exerted on the arrow, divide the work that has been done by the distance travelled in the direction of the force.

Apply unit conversion and ensure all quantities are measured in standard units:

• Mass of the arrow:
  `m = 15\; {\rm g} = 0.015\; {\rm kg}`.
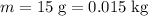• Distance travelled in the direction of the force:
  `s = 46.7\; {\rm cm} = 0.467\; {\rm m}`.

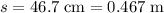At
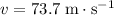`v = 73.7\; {\rm m\cdot s^(-1)}`, the kinetic energy of the
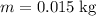`m = 0.015\; {\rm kg}` arrow would be
`(1/2)\, m\, v^(2)`.

Assuming that the arrow was initially stationary with a kinetic energy of
`0\; {\rm J}`. Subtract the original value of kinetic energy from the current value to find the change in kinetic energy:

`(\text{change in KE}) = (\text{current KE}) - (\text{initial KE})`.

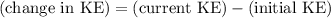By the Work-Energy Theorem, the amount of work done on the arrow would be equal to this change in kinetic energy.

To find average magnitude of the force, divide the amount of work done on the object by the distance travelled in the direction of the force:

`\begin{aligned}(\text{average force}) &= \frac{(\text{work done})}{(\text{distance travelled})} \\ &= \frac{(\text{change in KE})}{(\text{distance travelled})} && (\text{work-energy theorem})\\ &= \frac{(\text{current KE}) - (\text{initial KE})}{(\text{distance travelled})} \\ &= ((1/2)\, m\, v^(2) - 0)/(s) \\ &= ((1/2)\, (0.015)\, (73.7)^(2) - 0)/((0.467))\; {\rm N} \\ &\approx 87.2\; {\rm N}\end{aligned}`.

In other word, the average force on the arrow would be approximately
`87.2\; {\rm N}`.