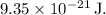The energy difference (
 ) between the n=0 and n=1 vibrational states for diatomic hydrogen is approximately
) between the n=0 and n=1 vibrational states for diatomic hydrogen is approximately
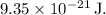
The energy difference (
 ) between vibrational states in a diatomic molecule can be calculated using the formula for harmonic oscillator energy levels:
) between vibrational states in a diatomic molecule can be calculated using the formula for harmonic oscillator energy levels:
![\[ \Delta E = h \cdot \\u \]](https://img.qammunity.org/2024/formulas/physics/college/3kylbdtsxya4h4pw2uyvje67ntne70pljg.png)
where:
- h is Planck's constant (
 ),
),
-
 is the vibrational frequency.
is the vibrational frequency.
For a diatomic molecule, the vibrational frequency (
 ) can be calculated using the formula:
) can be calculated using the formula:
![\[ \\u = (1)/(2\pi) \sqrt{(k)/(\mu)} \]](https://img.qammunity.org/2024/formulas/physics/college/e41msktcprp5he9vwkc48zq2a6hcslvzjo.png)
where:
- k is the force constant,
-
 is the reduced mass of the system.
is the reduced mass of the system.
The reduced mass (
 ) for a diatomic molecule can be calculated using:
) for a diatomic molecule can be calculated using:
![\[ \mu = (m_1 \cdot m_2)/(m_1 + m_2) \]](https://img.qammunity.org/2024/formulas/physics/college/83v2sfk1wehfzvf2nm71vbax2vk7thrqbc.png)
where:
-
 are the masses of the two atoms.
are the masses of the two atoms.
For diatomic hydrogen (
 ), each hydrogen atom has a mass of approximately
), each hydrogen atom has a mass of approximately
 (atomic mass units).
(atomic mass units).
Now, let's plug in the values:
![\[ \mu = \frac{(1.0079 \, \text{u})^2}{1.0079 \, \text{u} + 1.0079 \, \text{u}} \]](https://img.qammunity.org/2024/formulas/physics/college/nw5mze04cvyg4me5ifk665p4rzahvihbai.png)
![\[ \mu \approx 0.5039 \, \text{u} \]](https://img.qammunity.org/2024/formulas/physics/college/rqh28j98lxzukua473jtvde0dsqgaxc8j9.png)
![\[ \\u = (1)/(2\pi) \sqrt{\frac{576 \, \text{N/m}}{0.5039 \, \text{u}}} \]](https://img.qammunity.org/2024/formulas/physics/college/aeg9kngfbwq7vkaq5uzogjots2wmqezruu.png)
![\[ \\u \approx 1.412 * 10^(13) \, \text{Hz} \]](https://img.qammunity.org/2024/formulas/physics/college/1bda0o4x51ayrcgka4va4nv9h26crm8avd.png)
Now, calculate
 :
:
![\[ \Delta E = h \cdot \\u \]](https://img.qammunity.org/2024/formulas/physics/college/3kylbdtsxya4h4pw2uyvje67ntne70pljg.png)
![\[ \Delta E \approx (6.626 * 10^(-34) \, \text{J} \cdot \text{s}) \cdot (1.412 * 10^(13) \, \text{Hz}) \]](https://img.qammunity.org/2024/formulas/physics/college/2slgex6xhi7yfaw1g6jkpu99tcvziuxxmz.png)
![\[ \Delta E \approx 9.35 * 10^(-21) \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/college/suvhlszej1shv3zuel936upg2um5j3686r.png)
Therefore, the energy difference (
 ) between the n=0 and n=1 vibrational states for diatomic hydrogen is approximately
) between the n=0 and n=1 vibrational states for diatomic hydrogen is approximately