Question

P/q=1/2√x+a/x-a
Make x and a the subject of the formula and find the result

Answer 1

The result is x = a / (2 * (1 - P/Q)) and a= x(P−2Q(x−a))/P+2
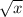`√(x)`a.

In the rearranged formula x= a/2(1− P/Q), the expression 1− P/Q represents the scaling factor, adjusting the impact of a on the value of x. As P and Q change, the denominator 2(1− P/Q) adapts, influencing the relationship between x and a. If P is significantly smaller than Q, the scaling factor approaches 1, and a has a more pronounced effect on x. Conversely, if P is close to Q, the scaling factor approaches 0, diminishing a's influence.

Step 1: Clear the fractions

P(x−a)=Q⋅2
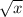`√(x)`(x−a)+a.2
`√(x)`

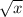
​Step 2: Simplify

Px−Pa=2Q
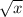`√(x)`(x−a)+2a
`√(x)`

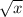
​Step 3: Isolate the terms

Px−2Q
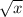`√(x)`(x−a)=Pa+2a
`√(x)`

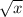
​Step 4: Solve for x and a

x(P−2Q(x−a))=a(P+2
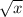`√(x)`a)

Solving for x:

x= a(P+2
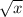`√(x)`a)/P−2Q(x−a)

Solving for a:

a= x(P−2Q(x−a))/P+2
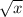`√(x)`a