Question

After fixing a flat tire on a bicycle you give the wheel a spin.

If its initial angular speed was 7.01 rad/s and it rotated 15.0 revolutions before coming to rest, what was itsaverage angular acceleration? (Consider speeding up postive and slowing down negative.)
_____rad/s².

Answer 1

The average angular acceleration of the wheel was -0.07437 rad/s².

To find the average angular acceleration (α), you can use the following kinematic equation:

`w^(2) _(f)` =
`w^(2) _(i)` + 2αθ

where:

`w_(f)` is the final angular speed (0 rad/s since it comes to rest),

`w_(i)` is the initial angular speed (7.01 rad/s),

α is the average angular acceleration (what we're trying to find),

θ is the angle rotated in radians (15 revolutions).

First, convert 15 revolutions to radians:

θ=15rev × 2πrad/rev

θ=30πrad

Now, plug in the values into the kinematic equation:

`0^(2)` =
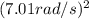`(7.01 rad/s)^(2)` + 2 ×α × (30πrad)

Solve for α:

2α × (30πrad) =
`(7.01 rad/s)^(2)`

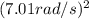
α =
`((7.01 rad/s)^(2))/(2×30πrad)`

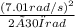
Now, calculate α:

α ≈ -0.07437 rad/s²

So, the average angular acceleration of the wheel was approximately -0.07437 rad/s²