The sum of the series is 567.
The sum of a finite geometric series is given by the formula:
![\[ S_n = (a_1(1 - r^n))/(1 - r) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1yfe4xfz7z3pvmcv98vvjzeb2i1xkydnfr.png)
where:
-
 is the sum of the series up to the n-th term,
is the sum of the series up to the n-th term,
-
 is the first term of the series,
is the first term of the series,
- r is the common ratio, and
- n is the number of terms.
In your case, the series is:
![\[ 9 + 18 + 36 + \ldots + 576 \]](https://img.qammunity.org/2024/formulas/mathematics/college/shp8nqer7ptx91qlm4nl7lq7rtqc9pn8bv.png)
It looks like a geometric series with
 (each term is obtained by multiplying the previous term by 2).
(each term is obtained by multiplying the previous term by 2).
The sum
 can be calculated using the formula. Since r = 2, the formula becomes:
can be calculated using the formula. Since r = 2, the formula becomes:
![\[ S_n = (9(1 - 2^n))/(1 - 2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/csju8i0wsh6ipnqztkkhwoz83ylcw043es.png)
Now, you mentioned the series goes up to 576, so we need to find n such that
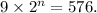
![\[ 2^n = (576)/(9) = 64 \]](https://img.qammunity.org/2024/formulas/mathematics/college/ip2o4j40wr0t99qbgw468igoqka1z8knnc.png)
Taking the logarithm base 2 of both sides:
![\[ n = \log_2(64) = 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/hox7zg2u9z98ppef1679di85yk5h644pjw.png)
Now, substitute n = 6 into the formula:
![\[ S_n = (9(1 - 2^6))/(1 - 2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/dq21vkssuldvbxr8jyqqvx8aub2y2wsrkd.png)
Calculate the expression to find the sum.
![\[ S_6 = (9(1 - 64))/(-1) \]](https://img.qammunity.org/2024/formulas/mathematics/college/6mnlevzlolxjyzepu4be9rsiatcmem6lkm.png)
![\[ S_6 = (9(-63))/(-1) = (-567)/(-1) = 567 \]](https://img.qammunity.org/2024/formulas/mathematics/college/vol9k70tpxu2cuaze3dwnorej28r75qx9k.png)
Therefore, the sum of the series is 567.