The points on the curve
 where the function f(x, y) = xy has extremum are:
where the function f(x, y) = xy has extremum are:
1.
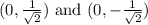
2.
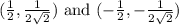
3.
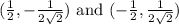
To find the points on the curve
 where the function f(x, y) = xy has extremum, we can use the method of Lagrange multipliers. The extremum points occur when the gradient of the function f is parallel to the gradient of the constraint
where the function f(x, y) = xy has extremum, we can use the method of Lagrange multipliers. The extremum points occur when the gradient of the function f is parallel to the gradient of the constraint
 .
.
Let's define the Lagrangian function:
![\[ L(x, y, \lambda) = xy + \lambda(1 - x^2 - 2y^2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1ynpyhfouo7xakdliouevtws2zw9kj5ymi.png)
Now, we need to find the partial derivatives of L with respect to
 , and set them equal to zero:
, and set them equal to zero:
1.
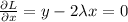
2.

3.
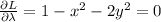
Solving this system of equations will give us the critical points.
Let's solve the system:
From equation (1), we have
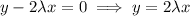
Substitute this into equation (2):
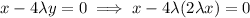
Simplify:
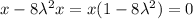
This gives two possibilities:
1. x = 0
2.
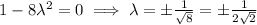
Now, we can use the third equation to find the corresponding values of y for each case.
For x = 0, we substitute into

For
 , substitute into
, substitute into
 to find the corresponding values of x and y.
to find the corresponding values of x and y.
Now, we have three sets of solutions for (x, y):
1.
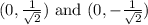
2. For
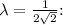
-
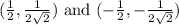
3. For
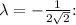
-
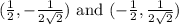
These are the points on the curve where the function f(x, y) = xy has extremum.
The probable question may be:
Find points of the curve x²+2y²=1 having extremum f(x,y)=xy