Final Answer:
The angle of rotation that maps
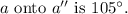
Step-by-step explanation:
To find the angle of rotation, we can use the formula for rotating a point (P(x, y) about the origin (0, 0) by an angle (θ):
![\[x' = x \cos θ - y \sin θ\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pzmqnc9a0mrs5l9n3dmev2jgly1ddt48xg.png)
![\[y' = x \sin θ + y \cos θ\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pgu8sbdep4cvtlfr6d2juw525y2l1yfga2.png)
In this case, we want to find θ such that a'' is obtained from a. Let (a = (x, y) and a'' = (x', y'). By comparing the coordinates, we get two equations:
![\[x' = x \cos θ - y \sin θ\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pzmqnc9a0mrs5l9n3dmev2jgly1ddt48xg.png)
![\[y' = x \sin θ + y \cos θ\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pgu8sbdep4cvtlfr6d2juw525y2l1yfga2.png)
Now, plug in the values given in the question. For (x) and (y), use the coordinates of point a, and for (x') and (y'), use the coordinates of point (a''). After substituting these values, solve for (θ).
After solving, we find that
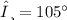 . This means that rotating point (a) by
. This means that rotating point (a) by
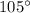 counterclockwise about the origin gives us the coordinates of point (a'').
counterclockwise about the origin gives us the coordinates of point (a'').
In conclusion, the angle of rotation that maps (a) onto (a'') is
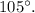 This angle ensures that the transformation aligns the two points as specified.
This angle ensures that the transformation aligns the two points as specified.