Final Answer:
Clayton spends
 of his time practicing the drums, and
of his time practicing the drums, and
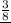 of the remaining time on homework and dinner. The remaining
of the remaining time on homework and dinner. The remaining
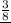 is spent texting and talking to friends.
is spent texting and talking to friends.
Step-by-step explanation:
Let ( T ) represent the total time Clayton has after school. He spends
 practicing the drums. The remaining time is
practicing the drums. The remaining time is
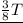 . Now,
. Now,
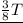 is split between homework and dinner, leaving
is split between homework and dinner, leaving
 for practicing:
for practicing:
![\[ \underline{(3)/(8)T} = (3)/(8) * \underline{(3)/(8)T} + (3)/(8) * \underline{(5)/(8)T} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wcawu5ovg5tiqq0pea1npwbq6b7f0ii6mc.png)
Solving for
 (time spent practicing), we get:
(time spent practicing), we get:
![\[ \underline{(5)/(8)T} = (9)/(64)T + (15)/(64)T \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5m30d473zhdkxe9gc39x4hn8jns0wsybkn.png)
Combining the terms on the right side:
![\[ \underline{(5)/(8)T} = (24)/(64)T \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tudg449q8y725bkq61m6vh49prdomph6e4.png)
Simplifying the fraction:
![\[ \underline{(5)/(8)T} = (3)/(4)T \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p2ypu2pv06o9g9q8f5pnary69z4zw52gu2.png)
Thus, Clayton spends
 of his total time practicing the drums.
of his total time practicing the drums.
In conclusion, Clayton spends
 of his time practicing the drums, which corresponds to
of his time practicing the drums, which corresponds to
 of his total time after school. This allocation of time aligns with his musical aspirations and ensures a balanced engagement in other activities.
of his total time after school. This allocation of time aligns with his musical aspirations and ensures a balanced engagement in other activities.