Question

When a window is open, the temperature in a room falls 5ºF every 15 minutes. Before the window is opened, the temperature was ​ 70ºF​ .

Use the Ray tool to make a graph that shows the temperature of the room, T, after the window has been open for m minutes.

Answer 1

The temperature (T) in a room decreases by 5ºF every 15 minutes after a window is opened, modeled by the linear equation
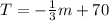`\(T = -(1)/(3)m + 70\)`, where m is the time in minutes. The graph is a straight line with a negative slope, starting at 70ºF.

The temperature (T) decreases by 5ºF every 15 minutes, indicating a linear decrease. We can use the slope-intercept form of a linear equation (y = mx + b) to represent this situation.

The initial temperature (b) is 70ºF, and the slope (m) represents the rate of change, which is
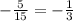`\(-(5)/(15) = -(1)/(3)\)` since the temperature falls by 5ºF every 15 minutes.

So, the equation representing the temperature (T) after m minutes of the window being open is:

`\[T = -(1)/(3)m + 70\]`

To visualize this on a graph, you can plot points for different values of m and T or use a graphing tool to input the equation. The graph would be a straight line with a negative slope, starting at 70ºF and decreasing by
`\((1)/(3)\)` per minute.