Final answer:
The correct answer to complete the inequality
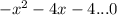
is '<' as the expression will always be less than zero for any real value of x.
Step-by-step explanation:
To complete the inequality
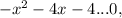
we need to determine the correct relational operator. Since the leading coefficient of the quadratic term

is negative, the parabola opens downward, which means it will always be less than a certain value depending on x. Therefore, for any value of x, the expression
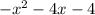
will always be less than zero. Thus, the correct answer to complete the inequality is < (Option 2).
Additionally, without specifically completing the square as per the provided context, we understand that the quadratic expression does not factor into a perfect square, and will not have a maximum value at zero for any real value of x. Hence, for all values of
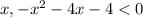
is the true statement.