Question

Afi loves to play the piano but doesn't like practicing the exercises his piano teacher assigns. There is a proportional relationship between the amount of time (in hours) that Rafi practices the piano, x, and how many cookies he gives himself, y. If x (hours) and y (cookies) are as follows:

1 4
2 8
3 12
8 32
What is the constant of proportionality? Write your answer as a whole number or decimal.

Answer 1

The constant of proportionality in the relationship between the time Rafi practices the piano (\(x\)) and the number of cookies he gives himself
`(\(y\))` is 4. Thus, the proportional equation representing this relationship is
`\(y = 4x\).`

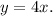
Step-by-step explanation:

In a proportional relationship, the ratio between the two variables remains constant. To find the constant of proportionality, we can take any pair of corresponding values for
`\(x\) and \(y\)` and calculate their ratio.

For instance, taking the pair (1, 4), we have
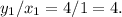`\(y_1/x_1 = 4/1 = 4\).` This ratio remains consistent for all the given pairs: (2, 8), (3, 12), and (8, 32). Therefore, the constant of proportionality is 4.

The proportional equation
`\(y = 4x\)` signifies that for every hour Rafi practices the piano
`(\(x\)),` he gives himself 4 cookies
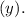`(\(y\)).` The pattern observed in the provided data aligns with this equation, confirming the proportional relationship.

This relationship implies that as the amount of practice time increases, the number of cookies awarded follows a consistent and linear growth.

Understanding proportional relationships is crucial in various mathematical applications. In this case, it helps quantify the connection between Rafi's practice time and his reward of cookies, providing a simple and direct mathematical model for the given scenario.