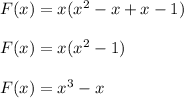Question

The graph of a function F is shown. Use the zeros and the turning points of the graph to find the rule for F.

Answer 1

By using the zeros and the turning points of the graph, the rule for F is
`F(x)=x^3-x`.

In Mathematics and Euclidean Geometry, a turning point refers to a point on the graph of a polynomial function in which it changes either from decreasing to increasing (falling to rising) or increasing to decreasing (rising to falling).

By cricitically observing the graph of the given polynomial function, we can logically deduce that the zeros are as follows;

x = -1 ⇒ (x + 1)

x = 0 ⇒ (x - 0) = x

x = 1 ⇒ (x - 1)

In this context, an exact equation that represent the polynomial function is given by:

F(x) = x(x + 1)(x - 1)

By expanding the polynomial function, we have;

`F(x) =x(x^(2) -x+x-1)\\\\F(x) =x(x^(2) -1)\\\\F(x)=x^3-x`