Answer:
a)

b)

Step-by-step explanation:
a) Let's use the conservation of linear momentum.

Where:
- m(b) is mass of bullet (0.03 kg)
- v(ib) is the initial velocity of the bullet (450 m/s)
- m(B) is the mass of the block (3 kg)
- v(f) is the final velocity of the bullet and the block


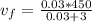

b) As we have an external force between B and C we can not use the conservation of linear momentum here. We need to use the work definition.
The work here is due to the friction force.

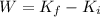


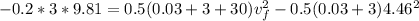
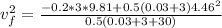
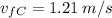
I hope it helps you!