The logarithmic function f(x) is increasing, passing through (1, 0), with a vertical asymptote at x = 0. Its domain is
 , and the range is
, and the range is
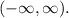
The given information describes a logarithmic function f(x) that is increasing, passes through the point (1, 0), and has a vertical asymptote at x = 0.
Domain:
The domain of a logarithmic function with a vertical asymptote at x = 0 is
 because logarithmic functions are undefined for non-positive values.
because logarithmic functions are undefined for non-positive values.
Range:
The range of an increasing logarithmic function is
 because as x increases, the function values also increase without bound.
because as x increases, the function values also increase without bound.
So, to match with the corresponding set of points:
- Domain: (0, ∞)
- Range: (-∞, ∞)
These sets represent the valid input values (domain) and the possible output values (range) for the given logarithmic function.