Answer:
Explanation:
Given that:
the sample proportion p = 0.39
sample size = 100
Then np = 39
Using normal approximation
The sampling distribution from the sample proportion is approximately normal.
Thus, mean
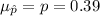
The standard deviation;
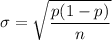
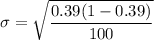
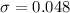
The test statistics can be computed as:
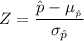
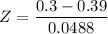

From the z - tables;
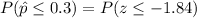
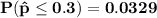
(b)
Here;
the sample proportion = 0.39
the sample size n = 400
Since np = 400 * 0.39 = 156
Thus, using normal approximation.
From the sample proportion, the sampling distribution is approximate to the mean
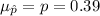
the standard deviation
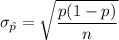
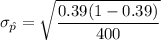
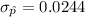
The test statistics can be computed as:
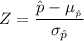
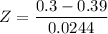

From the z - tables;
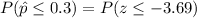
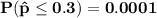
(c) The effect of the sample size on the sampling distribution is that:
As sample size builds up, the standard deviation of the sampling distribution decreases.
In addition to that, reduction in the standard deviation resulted in increases in the Z score, and the probability of having a sample proportion that is less than 30% also decreases.