Question

A pew research Center project on the state of news media showed that the clearest pattern of news audience growth in 2012 came on digital platforms. According to pew research data, 39% of Americans get news online or from a mobile device in a typical day. a. Suppose that you take a sample of 100 Americans. If the population proportion of Americans who get news online or from a mobile device in a typical day is 0.39, what is the probability that fewer than 30% in your sample will get news online or from a mobile device in a typical day? b. Suppose that you take a sample of 400 Americans. If the population proportion of Americans who get news online or from a mobile device in a typical day is 0.39, what is the probability that fewer than 30% in your sample will get news online or from a mobile device in a typical day? c. Discuss the effect of sample size on the sampling distribution of the proportion in general and the effect on the probabilities in (a) and (b).

Answer 1

Explanation:

Given that:

the sample proportion p = 0.39

sample size = 100

Then np = 39

Using normal approximation

The sampling distribution from the sample proportion is approximately normal.

Thus, mean
`\mu _(\hat p) = p = 0.39`

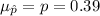
The standard deviation;

`\sigma = \sqrt{(p(1-p))/(n) }`

`\sigma = \sqrt{(0.39(1-0.39))/(100) }`

`\sigma = 0.048`

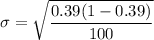
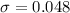
The test statistics can be computed as:

`Z = \frac{{\hat _(p)} - \mu_{_ {\hat p}} }{\sigma_(\hat p)}`

`Z = (0.3 - 0.39 )/(0.0488)`

`Z = -1. 8 4`

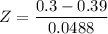
From the z - tables;

`P (\hat p \le 0.3 ) = P(z \le -1.84)`

`\mathbf{P (\hat p \le 0.3 ) = 0.0329}`

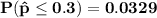
(b)

Here;

the sample proportion = 0.39

the sample size n = 400

Since np = 400 * 0.39 = 156

Thus, using normal approximation.

From the sample proportion, the sampling distribution is approximate to the mean
`\mu_(\hat p) = p = 0.39`

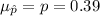
the standard deviation
`\sigma_(\hat p) = \sqrt{(p(1-p))/(n) }`

`\sigma_(\hat p) = \sqrt{(0.39 (1-0.39))/(400) }`

`\sigma_(\hat p) =0.0244`

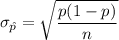
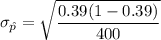
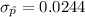
The test statistics can be computed as:

`Z = \frac{{\hat _(p)} - \mu_{_ {\hat p}} }{\sigma_(\hat p)}`

`Z = (0.3 - 0.39 )/(0.0244)`

`Z = -3.69`

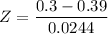
From the z - tables;

`P (\hat p \le 0.3 ) = P(z \le -3.69)`

`\mathbf{P (\hat p \le 0.3 ) = 0.0001}`

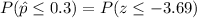
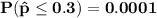
(c) The effect of the sample size on the sampling distribution is that:

As sample size builds up, the standard deviation of the sampling distribution decreases.

In addition to that, reduction in the standard deviation resulted in increases in the Z score, and the probability of having a sample proportion that is less than 30% also decreases.