Question

(a) Consider a class with 30 students. Compute the probability that at least two of them have their birthdays on the same day. (For simplicity, ignore the leap year.) (b) How many students should be in class in order to have this probability above 0.5

Answer 1

a.) 0.7063

b.) 23

Explanation:

a.)

Let X be an event in which at least 2 students have same birthday

Y be an event in which no student have same birthday.

Now,

P(X) + P(Y) = 1

⇒P(X) = 1 - P(Y)

as we know that,

Probability of no one has birthday on same day = P(Y)

⇒P(Y) =
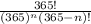`(365!)/((365)^(n) (365-n)! )` where there are n people in a group

As given,

n = 30

⇒P(Y) =
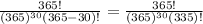`(365!)/((365)^(30) (365-30)! ) = (365!)/((365)^(30) (335)! )` = 0.2937

∴ we get

P(X) = 1 - 0.2937 = 0.7063

So,

The probability that at least two of them have their birthdays on the same day = 0.7063

b.)

Given, P(X) > 0.5

As

P(X) + P(Y) = 1

⇒P(Y) ≤ 0.5

As

P(Y) =
`(365!)/((365)^(n) (365-n)! )`

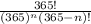
We use hit and trial method

If n = 1 , then

P(Y) =
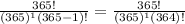`(365!)/((365)^(1) (365-1)! ) = (365!)/((365)^(1) (364)! )` = 1
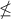`\\leq` 0.5

If n = 5 , then

P(Y) =
`(365!)/((365)^(5) (365-5)! ) = (365!)/((365)^(5) (360)! )` = 0.97
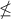`\\leq` 0.5

If n = 10 , then

P(Y) =
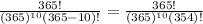`(365!)/((365)^(10) (365-10)! ) = (365!)/((365)^(10) (354)! )` = 0.88
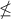`\\leq` 0.5

If n = 15 , then

P(Y) =
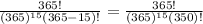`(365!)/((365)^(15) (365-15)! ) = (365!)/((365)^(15) (350)! )` = 0.75
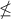`\\leq` 0.5

If n = 20 , then

P(Y) =
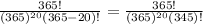`(365!)/((365)^(20) (365-20)! ) = (365!)/((365)^(20) (345)! )` = 0.588
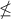`\\leq` 0.5

If n = 22 , then

P(Y) =
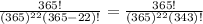`(365!)/((365)^(22) (365-22)! ) = (365!)/((365)^(22) (343)! )` = 0.52
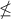`\\leq` 0.5

If n = 23 , then

P(Y) =
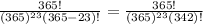`(365!)/((365)^(23) (365-23)! ) = (365!)/((365)^(23) (342)! )` = 0.49
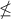`\\leq` 0.5

∴ we get

Number of students should be in class in order to have this probability above 0.5 = 23