Question

How long will it take to save ( $ 2329.00 ) by making deposits of ( $ 69.00 ) at the end of every three months into an account earning interest at ( 5 % ) compounded quarterly?

Answer 1

It will take approximately 8 years and 2 months to save $2329.00 by depositing $69.00 at the end of every three months into an account earning 5% interest compounded quarterly.

Step-by-step explanation:

To calculate the time needed to save $2329.00 by making deposits of $69.00 at the end of every three months at a 5% interest rate compounded quarterly, the formula for compound interest needs to be applied. The formula used here is
`A = P(1 + r/n)^((nt))`, where A represents the amount of money accumulated after n years, P is the principal amount (the initial deposit), r is the annual interest rate (in decimal), n is the number of times that interest is compounded per year, and t is the time in years.

Given:

P = $69.00 (deposit made at the end of every three months)

r = 5% or 0.05 (annual interest rate)

n = 4 (compounded quarterly)

A = $2329.00 (target amount)

Using the formula and solving for t:

2329 = 69(1 + 0.05/4)
`^{(4t)`

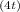
By rearranging the equation to solve for t:

(1 + 0.0125)
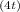`^{(4t)` = 2329 / 69

(1.0125)
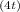`^{(4t)` = 33.7246

4t ≈ log(33.7246) / log(1.0125)

t ≈ log(33.7246) / (4 * log(1.0125))

t ≈ 8.17 years

Thus, it will take approximately 8 years and 2 months to save $2329.00 with these deposits and interest rates.