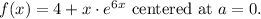Final Answer:
The Taylor series for f(x) = 4 + x * e^(6x) centered at a = 0 is:
![\[ f(x) = 4 + x + (6x^2)/(2!) + (6^2x^3)/(3!) + (6^3x^4)/(4!) + \dots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5paty5wzvhzfdscbn57c0n5xc16loxbcwz.png)
Step-by-step explanation:
The Taylor series for the function
 is an infinite sum that represents the function's values using the derivatives of the function evaluated at the center. In this case, the center is
is an infinite sum that represents the function's values using the derivatives of the function evaluated at the center. In this case, the center is
 The general form of the Taylor series is given by the formula:
The general form of the Taylor series is given by the formula:
![\[ f(x) = f(a) + f'(a)(x-a) + (f''(a))/(2!)(x-a)^2 + (f'''(a))/(3!)(x-a)^3 + \dots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wl2y621l7m6xntk0uvram0576axqnu94hk.png)
For the given function, the derivatives at
 are straightforward to calculate. The zeroth-order derivative
are straightforward to calculate. The zeroth-order derivative
 , the first-order derivative
, the first-order derivative
 is 1, and the higher-order derivatives follow a pattern related to the exponential function. The Taylor series is then constructed by plugging these values into the formula.
is 1, and the higher-order derivatives follow a pattern related to the exponential function. The Taylor series is then constructed by plugging these values into the formula.
The terms involving higher-order derivatives result in powers of
 in the series. As the series continues, each term involves a higher power of x and a higher power of 6, reflecting the behavior of the exponential term
in the series. As the series continues, each term involves a higher power of x and a higher power of 6, reflecting the behavior of the exponential term
 . Therefore, the final answer is the Taylor series representation of
. Therefore, the final answer is the Taylor series representation of