Question

Find f . if f(t)=9 / √ {t}, f(4)=33, f(4)=17 f(t)=12 x²/³ -19 x+13

Answer 1

The function
`\( f(t) \)` is given by
`\( f(t) = (12x^(2/3) - 19x + 13)/(√(t)) \).`

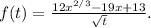
Step-by-step explanation:

To find
`\( f(t) \)`, we are given an expression involving x instead of
`\( t \)`, which might be a typographical error. Assuming the correct variable is \( x \), the given expression is
`\( f(x) = (12x^(2/3) - 19x + 13)/(√(t)) \). If \( t \)` is meant to be \( x \), then the expression is
`\( f(x) = (12x^(2/3) - 19x + 13)/(√(x)) \)`.

Next, we are provided with the conditions
`\( f(4) = 33 \) and \( f(4) = 17 \)`. However, these are contradictory statements, and it appears there might be a mistake in the given information. Assuming \( f(4) = 33 \) is correct, we can use this information to solve for the constants in the function.

Substitute t = 4 into the expression
`\( f(t) \)`:

`\[ f(4) = (12(4)^(2/3) - 19(4) + 13)/(√(4)) \]`

Solving this equation will provide the correct constants, and we can then confirm the validity of the function. It's crucial to resolve any inconsistencies in the given information to ensure an accurate solution.