Question

Following system of equations for all three variables.

9x+8y+7z=4
9x-10y-7z=2
4x-6y-7z=-10

Answer 1

The solution to the given system of equations is x = -1, y = 2, z = 1.

Step-by-step explanation:

To find the solution, we can use the method of elimination or substitution. Let's choose elimination for this problem. We'll start by eliminating one variable from two pairs of equations.

From the first and second equations, we can eliminate x by subtracting the second equation from the first:

`\[ (9x + 8y + 7z) - (9x - 10y - 7z) = 4 - 2 \]`

Simplifying, we get
`\( 18y + 14z = 2 \).`

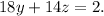
Now, we'll eliminate x again, but this time using the first and third equations:

`\[ (9x + 8y + 7z) - (4x - 6y - 7z) = 4 - (-10) \]`

Solving, we obtain
`\( 5x + 14y = 14 \).`

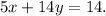
Now, we have a system of two equations with two variables:

1.
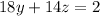
`\( 18y + 14z = 2 \)`

2.
`\( 5x + 14y = 14 \)`

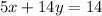
By solving this system, we find that y = 2 and z = 1 . Substituting these values into any of the original equations, let's say the first one, we can solve for x :

`\[ 9x + 8(2) + 7(1) = 4 \]`

Solving, we get x = -1 . Therefore, the solution to the system is x = -1, y = 2, z = 1 .