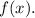Final Answer:
The correct form for the partial fraction decomposition of
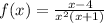 is option D:
is option D:
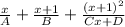 . This representation allows the expression to be split into three distinct fractions for integration purposes.D x/A + (x+1)/ B + (x+1)^2/ Cx+D
. This representation allows the expression to be split into three distinct fractions for integration purposes.D x/A + (x+1)/ B + (x+1)^2/ Cx+D
Step-by-step explanation:
The given rational function
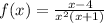 can be decomposed into partial fractions using the following form:
can be decomposed into partial fractions using the following form:
![\[f(x) = (A)/(x) + (B)/(x^2) + (C)/(x+1) + (Dx + E)/((x+1)^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zkzrr87vxnpm03er91dvvokccfq8wgiimc.png)
To find the unknown constants A, B, C, D, and E, you'll need to clear the denominators by multiplying both sides of the equation by
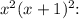
![\[x-4 = A(x+1)^2 + Bx(x+1) + Cx^2 + Dx^2 + Dx + E\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hjyp23bxb9jrobfk1tqnsl9g91008a9pjj.png)
Next, you can equate coefficients of like terms or strategically substitute values of x to solve for the unknowns.
Upon comparing coefficients, the equation reduces to:
![\[x-4 = (A + D)x^2 + (B + C + D)x + (A + E)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mlm7dr2jpdpuvbq3a2yg3r84rz3nbt0hs8.png)
By matching coefficients of similar powers of x, you'll obtain a system of equations to solve for A, B, C, D, and E.
Upon solving the system of equations, you'll find the values that satisfy the equations. The correct form for the partial fraction decomposition of
 is given by:
is given by:
![\[f(x) = (x)/(A) + (x+1)/(B) + (x+1)/(Cx+D)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2mpqc30qnlnhokbibouo2dlt5c1uqe9rbj.png)
Therefore, the correct choice among the options is **D x/A + (x+1)/ B + (x+1)^2/ Cx+D** as it accurately represents the partial fraction decomposition of