Question

g Suppose that a large mixing tank initially holds 500 gallons of water in which 50 pounds of salt have been dissolved. Another brine solution is pumped into the tank at a rate of 3 gal/min, and when the solution is well stirred, it is then pumped out at a slower rate of 2 gal/min. If the concentration of the solution entering is 2 lb/gal, determine a differential equation (in lb/min) for the amount of salt A(t) (in lb) in the tank at time t > 0. (Use A for A(t).)

Answer 1

the required differential equation is dA/dt -
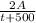`(2A)/(t+500)` = 6

A(0) = 50lb

Explanation:

Given the data in the question;

A(t) is the mass of the salt in in the tank at time t

the new volume of the solution in the tank increases by one gallon each minute

so

dA/dt = ( Rate in) - ( Rate out)

dA/dt = ( 3 gal/min × 2 lb/gal ) - ( 2 gal/min ×
`(A)/(t+500)` lb/gal )

dA/dt = 6 -
`(2A)/(t+500)`

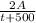
dA/dt -
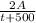`(2A)/(t+500)` = 6

A(0) = 50lb

Therefore, the required differential equation is dA/dt -
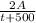`(2A)/(t+500)` = 6

A(0) = 50lb