Answer:
from the t-distribution table, at df = 7 and t = 2.23
Lies p-values [ 0.05 and 0.025 ]
Hence;
0.025 < p-value < 0.05
Explanation:
Given that;
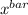 = 6.5 gpm
= 6.5 gpm
μ = 5 gpm
n = eight runs = 8
standard deviation σ = 1.9 gpm
Test statistics;
t = (
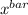 - μ) /
- μ) /
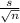
we substitute
t = (6.5 - 5) /
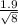
t = 1.5 / 0.67175
t = 2.23
the degree of freedom df = n-1 = 8 - 1
df = 7
Now, from the t-distribution table, at df = 7 and t = 2.23
Lies p-values [ 0.05 and 0.025 ]
Hence;
0.025 < p-value < 0.05