Question

A force of 192 lb is required to hold a spring stretched 3 ft beyond its natural length. How much work W is done in stretching it from its natural length to 6 inches beyond its natural length

Answer 1

The work done in stretching the spring is 8 lb.ft

Explanation:

Given;

Applied force, F = 192 lb

extension of the spring, x = 3 ft

Determine the spring constant from the applied force and extension;

`k = (F)/(x) \\\\k = (192 \ lb)/(3 \ ft) \\\\k = 64 \ lb/ft`

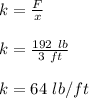
When the spring is stretched 6 inches beyond its natural length, the work done is calculated as follows;

x = 6 inches = 0.5 ft

`W = (1)/(2) kx^2\\\\W = (1)/(2) (64 \ lb/ft)(0.5 \ ft)^2\\\\W = 8 \ lb.ft`

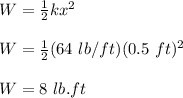
Therefore, the work done in stretching the spring is 8 lb.ft