Question

You can use the fact that is irrational to answer the questions below. You can also use other facts proven within this exercise. (a) Prove that is irrational. (b) Prove that is irrational. (c) Is it true that the sum of two positive irrational numbers is also irrational

Answer 1

See Explanation for proofs

Explanation:

Given

See attachment for complete question

Solving (a):

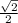`(√(2))/(2)` is irrational

`√(2) =1.41421356237.....`

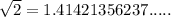
So, we have:

`(√(2))/(2) = (1.41421356237.....)/(2)`

`(√(2))/(2) = 0.70710678118....`

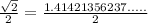
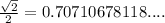
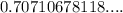`0.70710678118....` can not be represented as a fraction of whole numbers.

Hence:

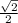`(√(2))/(2)` is irrational

Solving (b):

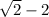`√(2) -2` is irrational

`√(2) =1.41421356237.....`

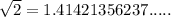
So, we have:

`√(2) -2 = 1.41421356237..... - 2`

`√(2) -2 = -0.58578643763.....`

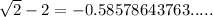
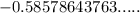`-0.58578643763.....` can not be represented as a fraction of whole numbers.

Hence:

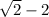`√(2) -2` is irrational

Solving (c):

The sum of two positive irrational number is always irrational

Proof Below

If a is irrational and b is also irrational,

then

`a + b = irrational`

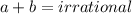
Take for instance:

`a = \sqrt{2`

`b = \sqrt{8`

`a + b = √(2) + \sqrt{8`

`a + b = √(2) + \sqrt{4*2`

`a + b = √(2) + √(4)*\sqrt{2`

`a + b = √(2) + 2\sqrt{2`

`a + b = 3\sqrt{2`

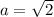
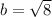
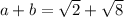
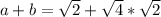
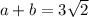
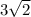`3\sqrt{2` is irrational and this is true for the sum of every positive irrational numbers