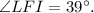Question

In the following diagram DE || FG and KL LFG. What is the measure of Zx? Angles are not necessarily drawn to scale.Given the following: D F I 20 A B K L 59° J E G​

Answer 1

To find the measure of angle
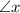`\( \angle x \)` in the given diagram, we can utilize the fact that corresponding angles are equal when a transversal intersects parallel lines. Since DE is parallel to FG, and KL is the transversal, we can set up an equation:

`\[ \angle JKL = \angle LFG \]`

Given that
`\( \angle JKL = 59^\circ \)`, we can substitute this value into the equation:

`\[ 59^\circ = \angle LFG \]`

Now, looking at the diagram, we can see that
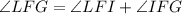`\( \angle LFG = \angle LFI + \angle IFG \)`. Given that
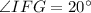`\( \angle IFG = 20^\circ \)`, we can substitute this into the equation:

`\[ 59^\circ = \angle LFI + 20^\circ \]`

Solving for
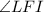`\( \angle LFI \)`, we get:

`\[ \angle LFI = 39^\circ \]`

Therefore, the measure of angle
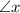`\( \angle x \)` is
`\( \angle LFI = 39^\circ \).`